Archive for the ‘flüssige Metalle’ Category
Wie kann man neuerdings wichtige Stoffdaten geschmolzener Metalle berechnen?
Montag, Juli 16th, 2018Posted in flüssige Metalle, Metallschmelzen und ihre Verbindungen, Sättigungsdaten von Metallschmelzen | Kommentare deaktiviert für Wie kann man neuerdings wichtige Stoffdaten geschmolzener Metalle berechnen?
Die Anwendung der neuen Peng- Robinson- Gleichung
Dienstag, Januar 16th, 2018Posted in flüssige Metalle, Peng-Robinson- Gleichung, Sättigungsdaten hochschmelzender Substanzen, Sättigungsdaten-Flüssigkeiten und Gase, Theorie der Flüssigkeiten und Gase, Zustandsgleichung | Kommentare deaktiviert für Die Anwendung der neuen Peng- Robinson- Gleichung
Die Anwendung einer allgemeinen Dampfdruckdifferentialgleichung
Donnerstag, Juli 28th, 2016






Posted in Allgemeine Dampfdruckdifferentialgleichung, Berechnung von Dampfdrücken, Dampfdruck von Kernbrennstoffen, Dichte von Flüssigkeiten und Gasen, Eisen, flüssige Metalle, Kernschmelze, Sättigungsdaten hochschmelzender Substanzen, Sättigungsdaten-Flüssigkeiten und Gase, Stoffdaten für Nuklearreaktoren, Theorie der Flüssigkeiten und Gase, Thermodynamik, Uran | Kommentare deaktiviert für Die Anwendung einer allgemeinen Dampfdruckdifferentialgleichung
Neue Ergebnisse zur Dampfdruckberechnung- angewendet auf flüssige Metalle und ihre Verbindungen bei der Kernschmelze
Freitag, Juni 10th, 20111. Ableitung einer allgemein gültigen Dampfdruckfunktion
Für die Verdampfungsenthalpie Δh eines Stoffes kann aus der thermodynamischen Theorie die Gleichung
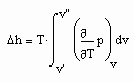
abgeleitet werden. Dabei ist T die absolute Temperatur / K, v‘ und v“ ist das molare Flüssigkeits- und das molare Sattdampfvolumen / cm³/mol dieses Stoffes. Die Funktion p(T,v) entspricht der Zustandsgleichung des jeweiligen Stoffes. Allerdings ist darauf hinzuweisen, daß die in der heutigen Technischen Thermodynamik meist angewendeten weitgehend halbempirisch genannten Zustandsgleichungen in obiger Δh- Gleichung gegenüber einer physikalisch begründeten van der Waals- Gleichung (s. „Stoffwerte von Flüssigkeiten und realen Gasen- berechnet mit Gesetzmäßigkeiten kritischer Phänomene“ – ISBN 978-3-00-027253-0) weniger genaue Ergebnisse liefern. Die angewendete Zustandsfunktion p(T,v) sollte entsprechend des Blog- Artikels vom 6.2.2010 („Die Zustandsdaten von Flüssigkeiten- berechnet von niedrigen bis hohen Drücken“) dem Gleichungssystem
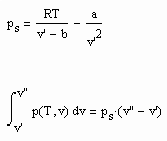
bei variablen Parametern a,b entsprechen, um genauere Ergebnisse zu erreichen (R=8.314 J/mol K- allgemeine Gaskonstante, ps- Dampfdruck).
Durch die Clausius- Clapeyronsche – Gleichung
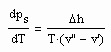 ,
,
die den Zusammenhang der Steigung der Dampfdruckkurve mit der Verdampfungsenthalpie und den Tau- und Siedevolumina v“,v‘ herstellt, ist eine allgemeine Dampfdruck- Differentialgleichung
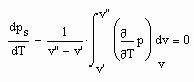
erklärt.
Diese Gleichung ist auswertbar. Die Auswertung der Differentialgleichung mit einem entsprechenden numerischen Lösungsprogramm als auch die Formulierung der analytischen Lösung ist möglich. Die Programme hierzu liegen vor.
Für Zustände niedriger bis mäßiger Drücke und den entsprechenden Temperaturen entsteht als allgemein gültige Differentialgleichung des Dampfdrucks
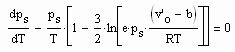 .
.
Dabei ist v’o das Siedevolumen der Flüssigkeit bei einer niedrigen Temperatur To, z. B. der des normalen Siedepunkts, b ist dann das Eigenvolumen des Stoffes ebenfalls bei der Temperatur To (s. o.gen. Literaturstellen).
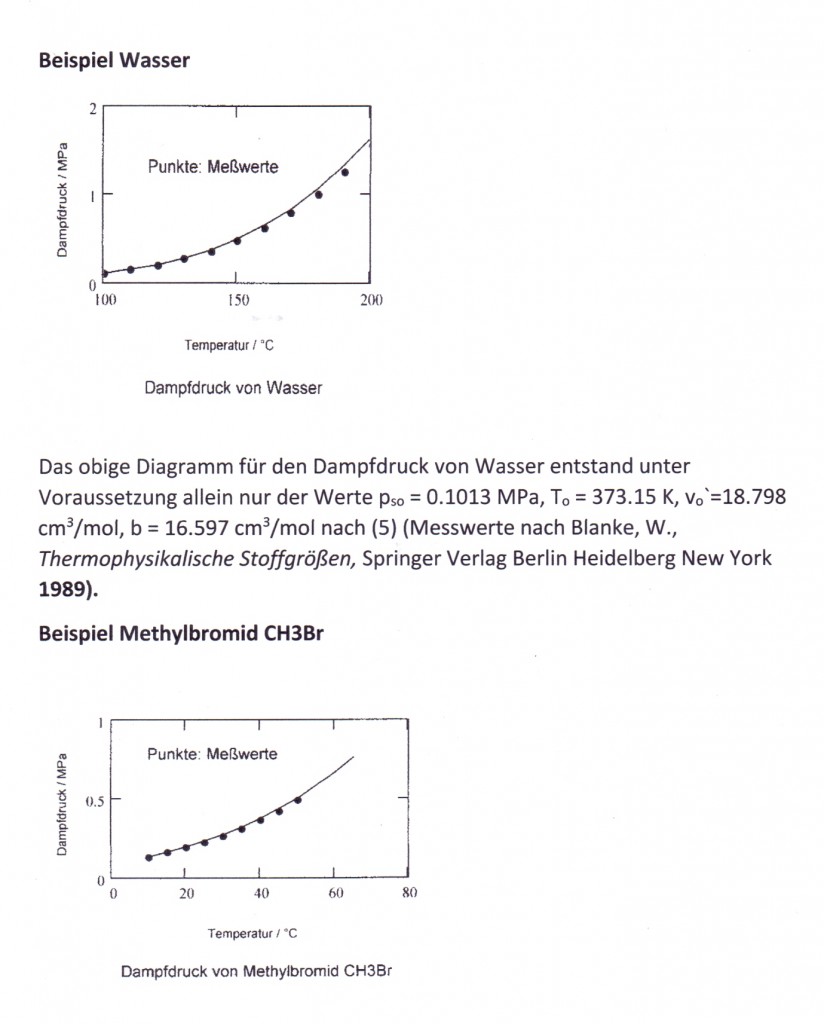
Die Lösung dieser mathematisch nicht ganz einfachen Gleichung (Funktionswert ps ist als nichtlinearer Term in der ln- Funktion enthalten) ist möglich. Man erhält tatsächlich immer recht gut mit Meßwerten übereinstimmende Dampfdruckwerte eines Stoffes. Voraussetzung ist die Kenntnis nur eines einzigen bekannten Datenpunktes als Meßwert. Dieser bekannte Datenpunkt kann der normale Siedepunkt To mit seiner Temperatur und dem molaren Flüssigkeitsvolumen sein. Man kann also mit obiger Dampfdruckdifferentialgleichung den Dampfdruckverlauf einer Substanz für Temperaturen unterhalb und oberhalb der normalen Siedepunktstemperatur problemlos rechnerisch bestimmen.
Es ist darauf hinzuweisen, daß mit allen anderen bisher angewendeten Dampfdrucknäherungen immer mehrere (ps,T)- Meßwerte (mindestens aber 2 bekannt sein müssen), um die Dampfdruckkurve innerhalb eines Temperaturintervalls angeben zu können.
2. Der Dampfdruck hochsiedender flüssiger Metalle und ihrer Verbindungen
Flüssige Metalle und ihre Verbindungen sind meist sehr hochsiedende Substanzen. Die Messung der Eigenschaften solcher Stoffe ist schwierig- allein schon wegen der Meßtechnik bei extrem hohen Temperaturen bis zu mehreren Tausend Kelvin.
Allerdings sind für etliche flüssige Metalle und ihre Verbindungen neben den Schmelztemperaturen auch normale Siedetemperaturen bekannt. Auch Dichten sind oftmals als Meßwerte vom Schmelzpunkt bis zu Temperaturen in Richtung des normalen Siedepunkts gegeben (aus z. B. sogen. „Wire Explosions in Air“ -Experimenten), so daß in diesen Fällen sogar Aussagen zum molaren Volumen bis zum normalen Siedepunkt möglich sind.
Damit sind grundsätzlich die Anfangsbedingungen (normale Siedetemperatur und molares Volumen am normalen Siedepunkt) zur Anwendung der o. gen. Dampfdruckdifferentialgleichung gegeben. In all diesen Fällen ist es möglich, den Dampfdruckverlauf flüssiger Metalle und ihrer hochsiedenden Verbindungen als Temperaturfunktion für Zustände unterhalb und oberhalb der normalen Siedetemperatur anzugeben.
Dies soll für einige besonders interessante Fälle im Zusammenhang mit möglichen Kernschmelzen geschehen.
3. Thermophysikalische Daten für Materialien im Zusammenhang mit Kernschmelzen
Die kürzlichen Vorgänge in japanischen Kernkraftwerken, die -wie sich nun noch nachträglich herausstellt- sogar bis zu Kernschmelzen führten, rücken die Atomkraft wieder vermehrt in das öffentliche Interesse.
Die Fragen zur Beherrschbarkeit der Atomtechnologie im Havariefall sind berechtigt. Für den Fall der Kernschmelze und der damit bei ungenügender Kühlung weiter steigenden Temperatur ist es wichtig, die Eigenschaften der beteiligten Materialien genau zu kennen. Dies betrifft vor allem die Brennstäbe mit z. B. den Materialien Urandioxid, Plutoniumdioxid und Zirkonium. Es ist zu fragen, ob die thermophysikalischen Eigenschaften dieser hochschmelzenden Materialien überhaupt genügend bekannt sind. Als fundamentale Materialeigenschaften sollten zur Ermöglichung einer Voreinschätzung des Verlaufs einer möglichen Kernschmelze zumindest bekannt sein: Schmelzpunkt, normaler Siedepunkt, Dichten des Feststoffes bis zum Schmelzpunkt, Dichten der Schmelze oberhalb der Schmelztemperatur entlang der Siedelinie, Dampfdrücke bis zur normalen Siedetemperatur und darüber.
Sehr wichtig im Fall der Kernschmelze ist die Eigenschaft des sich bildenden Schmelzsees der beteiligten Materialien im System einer entstehenden Mischungslücke von U-Zr-O- Fe bzw. von Tendenzen der Verhinderung einer Entmischung durch Konvektionsströmungen in der Schmelze. Gerade aber in diesem Fall ist die Kenntnis thermophysikalischer Daten – wie z. B. des Dampfdrucks- der einzelnen Komponenten des Gemisches zur Beurteilung insgesamt der flüssigen Phase und der Gasphase als nichtideales Gemisch von ausschlaggebender Bedeutung. (Datenbanken s. GEMINI, NUCLEA, CHEMSA/ CHEMAPP, MOX)
Die Frage ist, ob das alles für die beteiligten Stoffe bekannt ist und vorliegt und genügend genau in relevanten Simulationsprogrammen für Kernschmelzen erfasst ist. Wer weiß das schon wirklich mit dem Nachweis der ausreichenden Genauigkeit oder ist die ausreichende Genauigkeit nur eine Behauptung?
Aus allgemein zugänglichen Datensammlungen (z. B. „Detherm“ der Dechema, „webelements.com“ u. a.) und speziellen mit flüssigen Metallen befassten Literaturstellen ergeben sich solche Daten leider in der vollständigen Gänze nicht und im Detail sogar widersprüchlich.
Evtl. ist es so, daß interne und nicht allgemein zugängliche Betreiber- und Firmendaten vorliegen.
Bekannt ist, daß es intensive Forschungsbemühungen gab, thermophysikalische Eigenschaften hochschmelzender Metalle durch Wire Explosions in Air- Experimente zu erfassen. Dadurch wurden Angaben zur elektrischen Leitfähigkeit und auch zur Dichte bei hohen Temperaturen gewonnen. Auch physikalisch- theoretische Untersuchungen zur kritischen Temperatur, zum kritischen Druck und zum evtl. Verlauf der Dampfdruckkurve als Extrapolation von niedrigen Meßwerten aus liegen vor (s. z.B. die Arbeiten von H. Hess, H. Schneidenbach in Z. Metallkunde).
All diese Untersuchungen und Ergebnisse belegen letztlich die für flüssige Metalle unbefriedigende Situation, thermophysikalische Daten nicht oder nur ungenau zu kennen. Auch für die Verbindungen dieser Metalle und für ihre Mischungen trifft das trotz der umfangreichen jeweils staatlichen Mittelzuflüsse für Forschungen dieser Art zu, die der Steurerzahler bezahlen mußte.
Sollte es evtl. nur eine Hoffnung sein, anzunehmen. daß AKW- Betreiberfirmen einen weiterführenden Datenbestand zu Kernreaktor- Materialien haben?
Die Anwendung der o. gen. physikalisch begründeten Dampfdruck- Differentialgleichung , deren Richtigkeit an vielen anorganischen und organischen Substanzen nachgewiesen werden kann, muß auch im Fall flüssiger Metalle und seinen Verbindungen gerechtfertigt sein. Das kann nachgewiesen werden.
Für einige flüssige Metalle liegen physikalisch und versuchstechnisch begründete Ergebnisse zum Dampfdruckverlauf und zur Dichte für Temperaturen über dem Schmelzpunkt vor. Wenn sich zeigt, daß die bisher in der Literatur als Näherungen für solche Metalle angegebenen Dampfdruckkurven mit Lösungen der o.gen. Dampfdruck- Differentialgleichung übereinstimmen, ist wohl erklärt, diese Differentialgleichung tatsächlich zur Bestimmung von Dampfdrücken flüssiger Metalle und ihren hochsiedenden Verbindungen einsetzen zu können.
Für zwei wichtige Metalle, zu denen genügend Untersuchungsergebnisse vorliegen, soll das gezeigt werden- nämlich für Uran und Eisen.
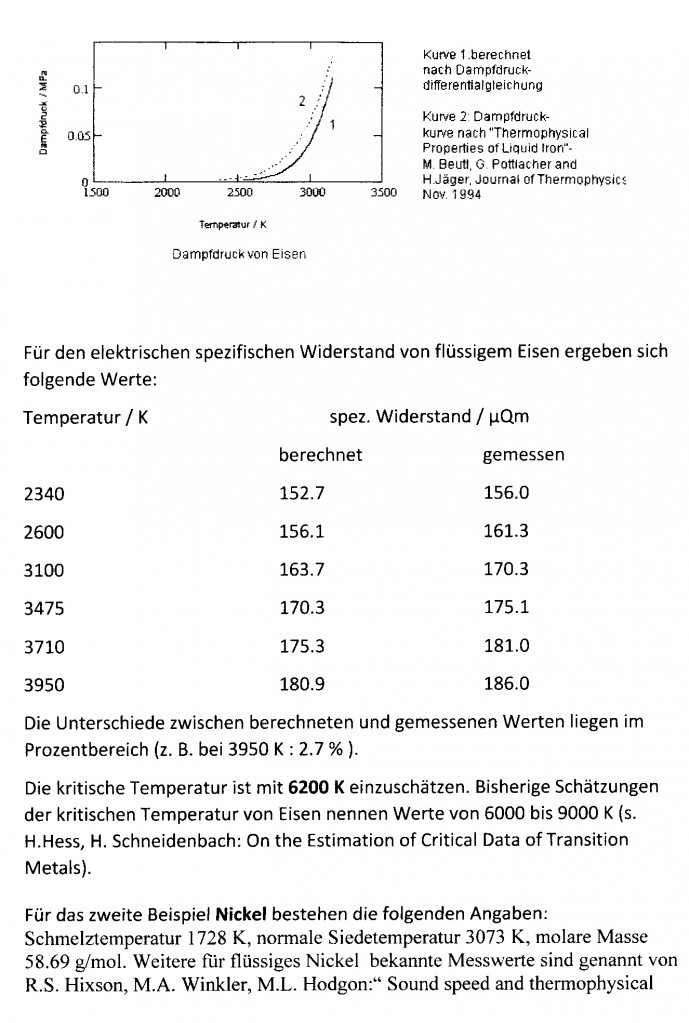
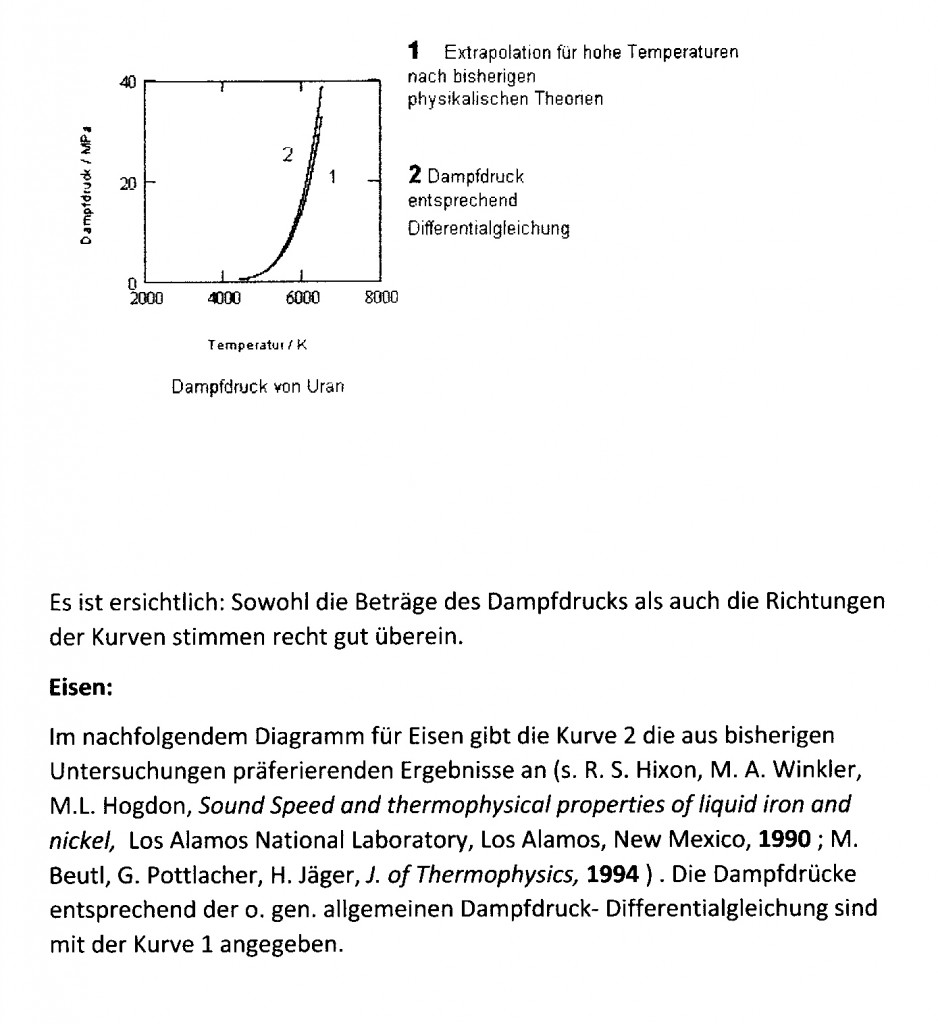
Der für Uran erwartete Dampfdruckverlauf wird in einer den bisherigen Kenntnisstand zusammenfassenden Arbeit „Vapor pressure and critical Data for Uranium“ von H. Hess, H. Schneidenbach (Z. Metallkunde 92, 2001) dargestellt. Diese Arbeit gibt die Ergebnisse verschiedener Forscher vergleichend an. Die für Uran nach Meinung der Autoren präverierende Dampfdruckkurve wird angegeben. In nachfolgendem Diagramm ist das die Kurve 1 . Die aus der o.gen. allgemeinen Differentialgleichung sich ergebenden Dampfdruckwerte für Uran sind in der Kurve 2 erfaßt.
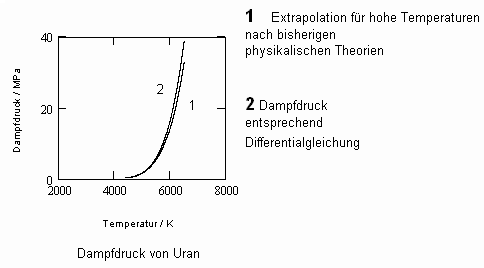
Es ist ersichtlich: Sowohl die Ordinatenwerte als auch die Steigungen beider Kurven stimmen recht gut überein.
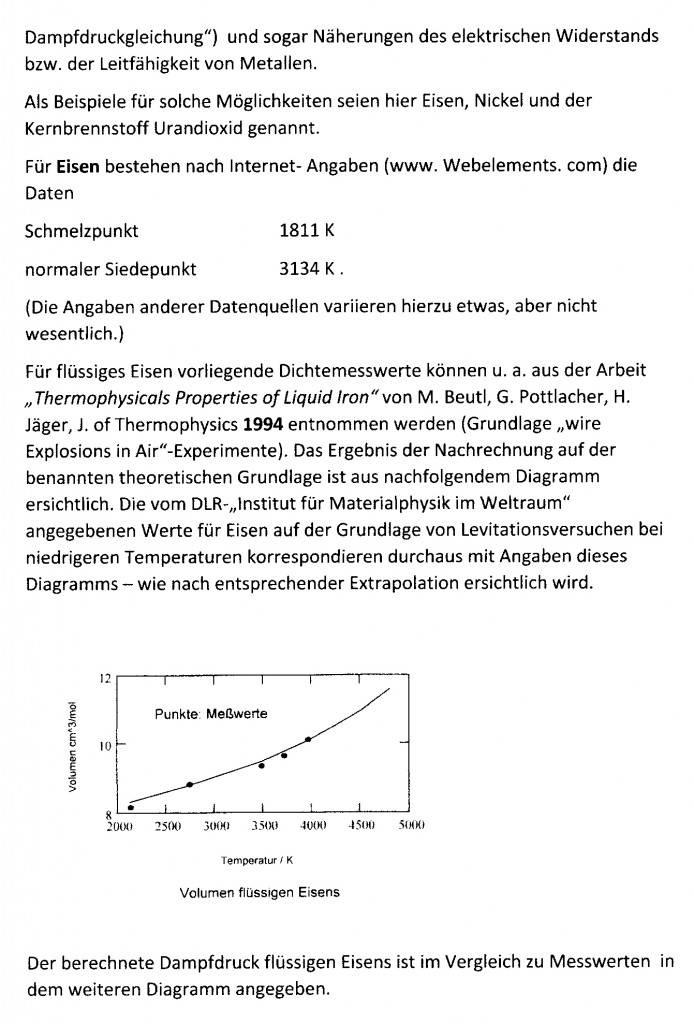
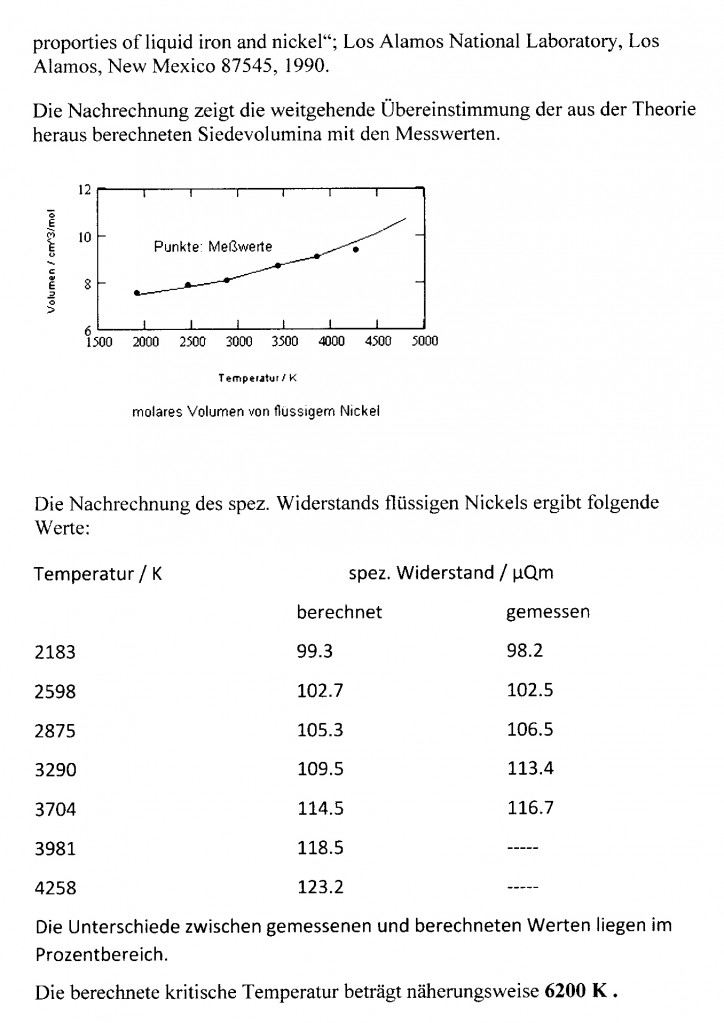
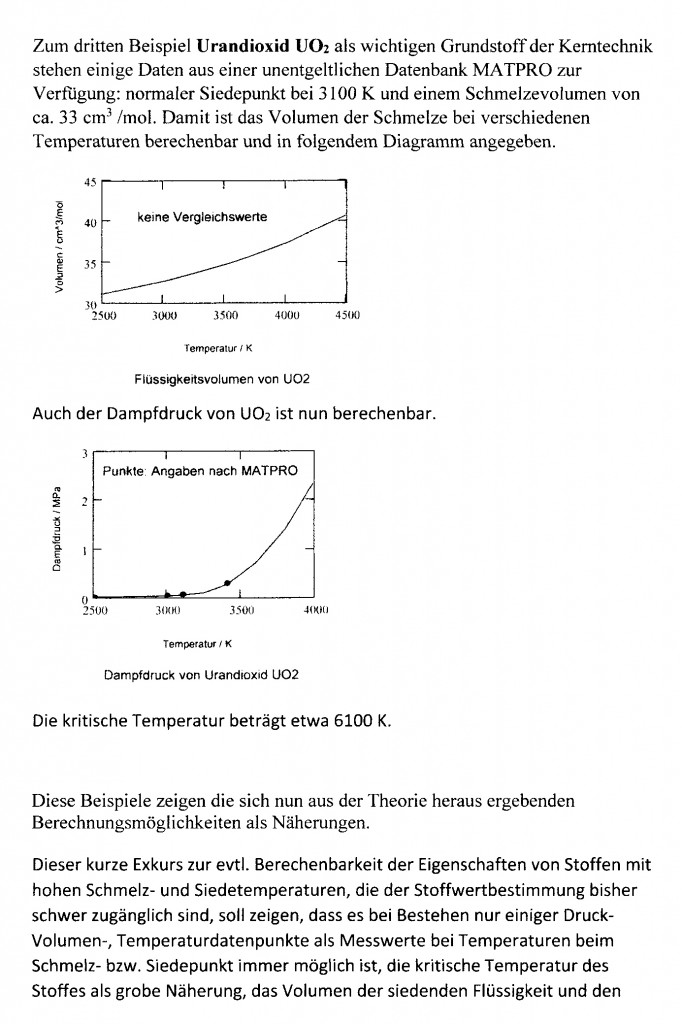
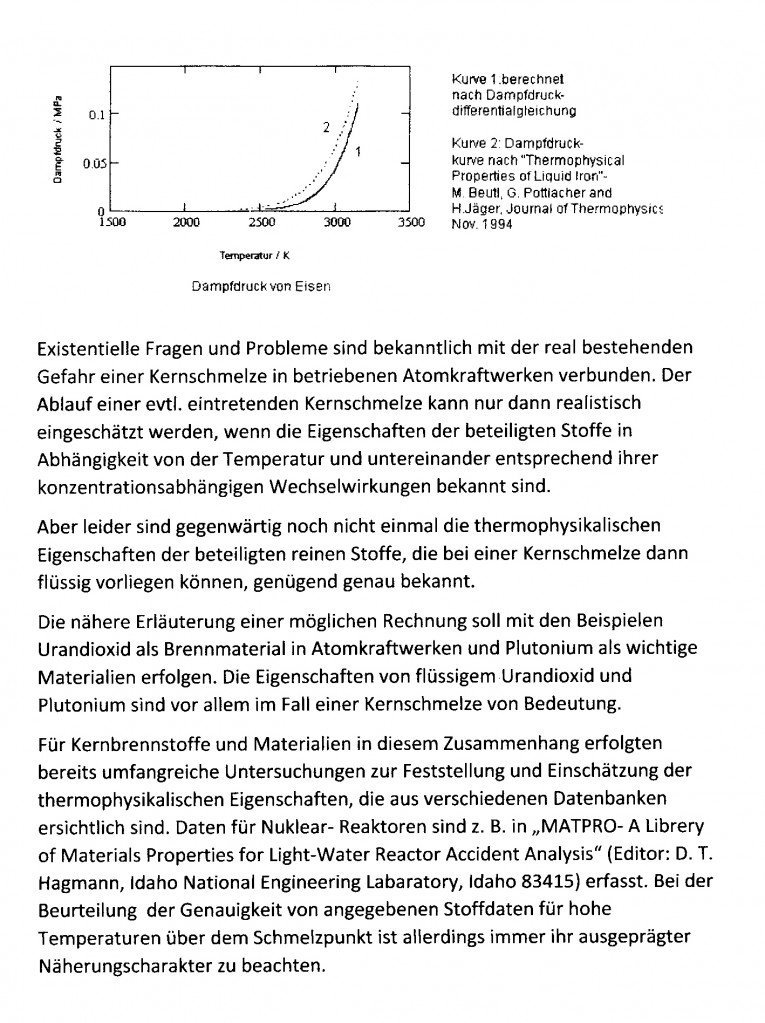
Auch für Eisen im flüssigen Zustand ist das etwa so feststellbar, wie das nachfolgende Diagramm zeigt.
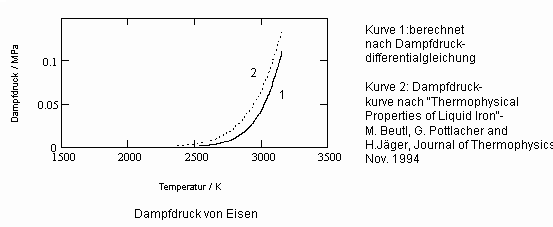
Ergänzend ist zu sagen: Auch die Nachrechnung weiterer Beispiele flüssiger Metalle mit entsprechend bekannten Daten bestätigt die Anwendbarkeit der o. gen. Dampfdruck-Differentialgleichung. Es muß dazu jeweils nur ein Dampfdruckmeßwert und das molare Volumen bei der Meßtemperatur bekannt sein.
Es ist deshalb gerechtferigt, die o.gen. Dampfdruck-Differentialgleichung auch auf radioaktive flüssige Uran- und Plutoniumverbindungen, wie Urandioxid und Plutoniumdioxid, auf flüssiges Plutonium und Zirkonium anzuwenden.
Plutonium:
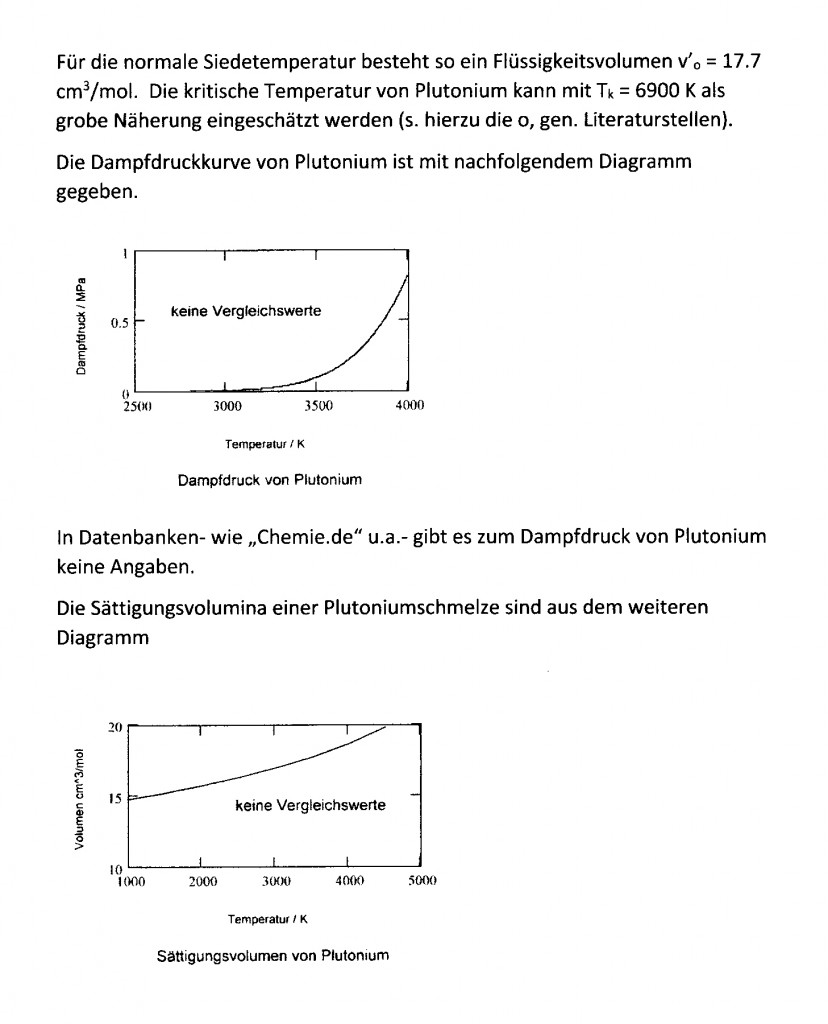
Molekülmasse: 244.0642, Schmelzpunkt: 912.5 K, Siedepunkt: 3509 K, Dichte 16.63 g/cm³ bei 914 K (s. www.webelements.com, David R. Lide: CRC Handbock of Chemistry and Physics, 90 th Edition, CRC Press, Boca Raton, Florida 2009)
Mit diesen Daten als Ausgangspunkt der Rechnung ergibt sich das nachfolgende Diagramm als Näherung für den Verlauf der Dampfdruckkurve von Plutonium bei hohen Temperaturen.
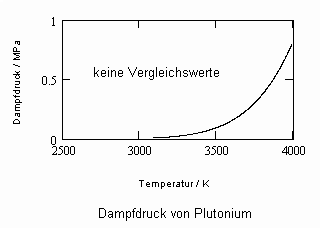
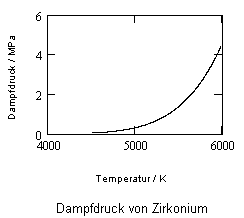
Zirkonium:
Molekülmasse: 91.224, Schmelzpunkt: 2128 K, Siedepunkt: 4682 K, Dichte (s.): 6.511 g/cm³ (s. www.webelements.com)
Die Dampfdrucknäherung von Zirkonium ist mit nachfolgendem Diagramm gegeben.
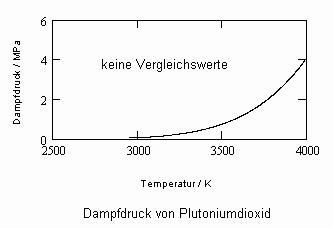
Plutoniumdioxid PuO2:
Molekülmasse 276.06, Schmelzpunkt 2673 K, Siedepunkt 3073 K, Dichte (s) 11.50 g/cm³ (s. www.webelements.com).
Das diesen Daten entsprechende Dampfdruckdiagramm ist die folgende Näherung:
Urandioxid:
Molekülmasse: 270.03, Schmelzpunkt: 2827 °C, Siedepunkt:- , Dichte (s): 10.97 g/cm³ (s. www.webelements.com, GESTIS-Stoffdatenbank des IFA)
Leider liegt zur Berechnung der Dampfdruckkurve von Urandioxid kein vollständiger p,v,T- Datensatz vor. Die Dampfdruckkurve kann so nicht angegeben werden.
Posted in flüssige Metalle, Kernschmelze | Kommentare deaktiviert für Neue Ergebnisse zur Dampfdruckberechnung- angewendet auf flüssige Metalle und ihre Verbindungen bei der Kernschmelze
Flüssige Metalle
Freitag, November 12th, 2010Metalle im flüssigen Zustand sind wegen ihrer überwiegend hohen bis sehr hohen Temperaturen versuchstechnisch schwierig oder gar nicht zu erfassen. Die pvT- Daten flüssiger Metalle sind nur ungenügend bekannt. Es ist deshalb kaum möglich, die Anwendbarkeit üblicher Zustandsgleichungen, z. B. die van der Waals- Gleichung oder die empirischen Gleichungen von Redlich- Kwong, Peng- Robinson u.a. zur Berechnung von Stoffdaten flüssiger Metalle anzuwenden oder zu prüfen.
Wie soll man z. B. die Anwendbarkeit der von der Waals- Gleichung prüfen, wenn die kritischen Daten eines Metalles nicht bekannt sind? Wie soll man die Anwendbarkeit der heute weltweit benutzten Soave- Redlich-Kwong- Gleichung prüfen, wenn weder die kritischen Daten, noch der azentrische Faktor bekannt sind? Wie soll man sinnvoll berechnete Dampfdrücke flüssiger Metalle voraussetzen, wenn diese Drücke nicht gemessen werden können? Weitere solche Fragen bestehen für flüssige Metalle, z. B. erst recht für nahkritische und überkritische Zustände.
Im Artikel „Die Berechnung von Dampfdrücken“ vom 11.12. 2009 und speziell in der Veröffentlichung „Stoffwerte von Flüssigkeiten und realen Gasen- berechnet mit Gesetzmäßigkeiten kritischer Phänomene“ (ISBN 978-3-027253-0 , 2009) wird die Möglichkeit erklärt, die kritischen Daten eines Stoffes als grobe Näherung zu berechnen, wenn nur Dampfdruck und Volumen bzw. Dichte- Angaben für diesen Stoff bei niedrigen Druck und entsprechend niedriger Temperatur bekannt sind. Ausreichend für die grob näherungsweise Berechnung der kritischen Temperatur ist schon die Kenntnis nur der normalen Siedetemperatur und des molaren Volumens am normalen Siedepunkt.
Die normale Siedetemperatur ist für alle Metalle bekannt- entweder als Meßwert oder als Schätzwert für die hochsiedenden Metalle- wie z. B. Wolfram u.a.
Die Dichten bzw. Volumina der flüssigen Metalle am normalen Siedepunkt sind als Meßwerte bekannt (Messung unter Siedebedingungen bzw. durch sogen. „Wire Explosions in Air“).
Die kritischen Daten der Metalle können damit als grobe Näherungen entsprechend der Berechnungsgleichungen, die in der Veröffentlichung „Stoffwerte von Flüssigkeiten und realen Gasen- berechnet mit Gesetzmäßigkeiten kritischer Phänomene“ abgeleitet sind, eingeschätzt werden. Mit der in diesem Zusammenhang angegebenen grundsätzlichen Beziehung
![]()
zwischen dem molaren Siede- und dem Tauvolumen v‘, v“ bei der jeweiligen Temperatur T und der kritischen Temperatur Tk (β – kritischer Exponent, Kv – Konstante) besteht die Möglichkeit zur Berechnung des Flüssigkeitsvolumens v‘ , wenn das Tauvolumen v“ bekannt ist. Da das Tauvolumen ebenfalls mit einer aus der Theorie kritischer Phänomene ableitbaren Beziehung berechnet werden kann (s. o. gen. Veröffentlichung), ist so sowohl das Volumen bzw. die Dichte des flüssigen Metalls als auch das Dampfvolumen entlang der Dampfdruckkurve als Temperaturfunktion bekannt. Zu betonen ist, daß es sich hierbei um Näherungen handelt, die mit steigender Temperatur ( in Richtung der kritischen Temperatur) ungenauer werden. Die berechneten Volumen- und Dichtedaten für niedrige Temperaturen flüssiger Metalle (vom Schmelzpunkt bis weit über den normalen Siedepunkt hinaus) entsprechen allerdings recht gut verfügbaren Meßwerten.
In nachfolgenden Artikeln können nun entsprechend dieser Erklärung für einzelne flüssige Metalle in Diagrammform die molaren Volumina für die siedende Flüssigkeit und den entsprechenden Sattdampf in Abhängigkeit von der Temperatur angegeben werden.
Posted in flüssige Metalle | Kommentare deaktiviert für Flüssige Metalle