Dioxan ist ein organischer Stoff polaren Charakters.
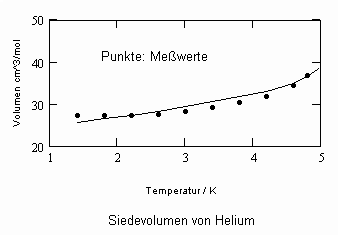
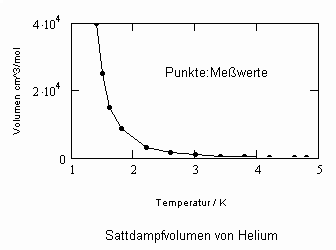
Die Nachrechnung der Sättigungsdaten für den Dampf und die Flüssigkeit kann auch für diesen Stoff nur allein mit den Angaben zum kritischen Punkt und zum normalen Siedepunkt erfolgen. Dies geschieht mit den die Berechnungsgrundlagen angebenden Gleichungen im Artikel „Stoffwerte von Flüssigkeiten und realen Gasen- berechnet mit Gesetzmäßigkeiten kritischer Phänomene“ vom 7.5.2009.
Die verwendeten Daten sind folgende: Kritische Temperatur- 587.0 K, kritischer Druck- 5.2777 MPa, normaler Siedepunkt- 374.55 K, Flüssigkeitsvolumen am normalen Siedepunkt- 93.943 cm³/mol, Dampf-volumen am normalen Siedepunkt- 30740 cm³/mol.
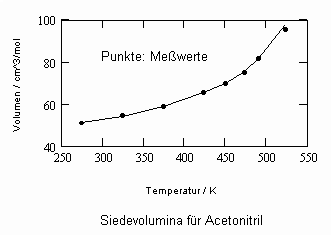
Die für Dioxan berechneten Siede- und Tauvolumina sind in den beiden nachfolgenden Diagrammen als Näherungen angegeben.
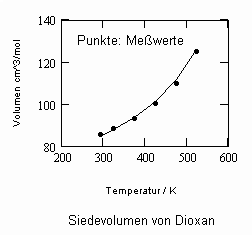
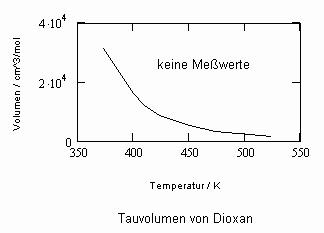
Auch berechnete Realgasfaktoren Z = pv/RT (R- allgemeine Gaskonstante 8.314 J/mol K) für einige Temperaturen und vorgegebene Drücke sind exemplarisch genannt.
Temperatur: 423.15 K (150 °C)
Druck /MPa 0.1 0.5 1.0 5.0 10.0
Realg. fakt. 0.99 0.014 0.029 0.143 0.284
Temperatur: 473.15 K (200°C)
Druck /MPa 0.1 0.5 5.0 10.0
Realg.fakt. 0.99 0.94 0.14 0.28
Die Berechnung weiterer Realgasfaktoren zur Einschätzung des Flüssigkeits- und Gasverhaltens von Dioxan ist mit den abgeleiteten Gleichungen ohne weiteres möglich.