Speziell für Flüssigkeiten kann physikalisch begründet die Zustandsgleichung
![]()
abgeleitet werden. Dabei ist T die absolute Temperatur / K , p der Druck über der Flüssigkeit / MPa, ps der Dampfdruck der Flüssigkeit/ Mpa, v das molare Volumen/ cm³/mol, b das molekulare Eigenvolumen/ cm³/mol und K eine dimensionslose Konstante. Diese Gleichung gilt für Flüssigkeiten entsprechend Temperaturen niedriger Dampfdrücke bis zu Temperaturen höherer Dampfdrücke, nicht aber in der Nähe der kritischen Temperatur.
Das Moleküleigenvolumen b ist als die Summe der einzelnen Volumina, die die Moleküle des Stoffes durch ihre atomare Strucktur im Raum aufspannen, erklärt. Das Eigenvolumen erweist sich über weite Temperaturbereiche (von niedrigen bis zu hohen Temperaturen, nicht aber in der Nähe der kritischen Temperatur) als konstant. Es kann mit Stoffdaten, die für niedrige Dampfdrücke gelten, berechnet werden- z. B. mit den (p,v,T)- Daten des oft bekannten normalen Siedepunkts, ebenso ist auch die obige Größe K festgelegt. Zu den Einzelheiten der Theorie s. “ Stoffwerte von Flüssigkeiten und realen Gasen- berechnet mit Gesetzmäßigkeiten kritischer Phänomene“ (ISBN 978-3-00-027253-0).
Für etliche technisch wichtige Stoffe sind die sogen. Realgasfaktoren Z = pv/RT sowohl für die Gas- als auch für die Flüssigphase entlang einer Isotherme von niedrigen bis zu hohen Drücken erfaßt. Diese Daten sind aus Stoffdatenbanken oder aus Stoffwertsammlungen (s. z. B. W. Blanke: „Thermophysikalische Stoffgrößen“, Springer Verlag) zu entnehmen. Es handelt sich um versuchstechnisch ermittelte Werte. Die Nachrechnung dieser Werte mit den heute in physilalischer Chemie und Verfahrenstechnik bekannten Zustandsgleichungen führt oft zu Ergebnissen, die mit den Meßwerten nicht übereinstimmen. Vor allem bei Flüssigkeiten ist das so, da es für Flüssigkeiten bisher keine allgemein anwendbare und physikalisch begründete Zustandsgleichung gab. Die o.gen. Flüssigkeits- Zustandsgleichung ermöglicht es allerdings nun, Flüssigkeitsvolumina bei vorgegenem Druck und gegebener Temperatur bei weitgehender Übereinstimmung mit Meßwerten zu berechnen bzw. die Realgasfaktoren zu bestimmen.
Die Tatsache, daß die bisher auch für Flüssigkeiten angewendeten Zustandsgleichungen von van der Waals und ihre Modifikationen zu oft ungenauen Ergebnissen führen, ist als Theorie- Tatsache durchaus bekannt, da es eine physikalisch ausgearbeitete Theorie der Flüssigkeiten bisher nicht gibt. Interessant ist deshalb das Ergebnis einer Umfrage zu diesem Thema. Es wurde die Frage gestellt, ob es unterdessen Möglichkeiten zur Berechnung von Flüssigkeits- Realgasfaktoren bis zu hohen Drücken von 50 bis 100 MPa mit geringen Fehlern gegenüber Ergebnissen aus Meßwerten gibt. Es wurde gefragt: Ist es überwiegend in der Praxis noch so, daß für Flüssigkeiten nur eigens durchgeführte pvT- Messungen zum Ziel führen? Fachlich fundierte Antworten bestätigten, daß es bisher noch keine physikalisch begründeten allgemein gültigen Ergebnisse aus einer Theorie der Flüssigkeiten gibt, die es ermöglichen würde, Realgasfaktoren für Flüssigkeiten vom Dampfdruck bis zu hohen Drücken auf einer Isotherme mit ausreichender Übereinstimmung mit Meßwerten zu berechnen.
Aber es gab auch ganz andere Antworten. Z. B. die, man solle dazu unter „google scholar“ nachsehen. Oder gar keine Stellungnahmen. Oder die: Es gibt Berechnungsmöglichkeiten.
Die o. gen. speziell für Flüssigkeiten bestehende Gleichung wurde mit einer Vielzahl von Stoffbeispielen immer mit dem Ergebnis weitgehender Übereinstimmung mit Meßwerten überprüft. Einige Beispiele dazu sind im Artikel “ Erdgas- flüssig “ vom 4.3. 2010 bereits genannt. Vor allem ist auf den Artikel „Die Zustandsdaten von Flüssigkeiten- berechnet von niedrigen bis hohen Drücken“ vom 6.2.2010 in diesem Zusammenhang hinzuweisen.
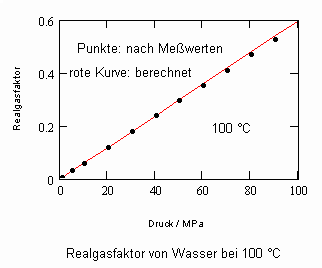
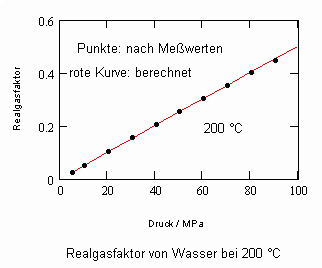
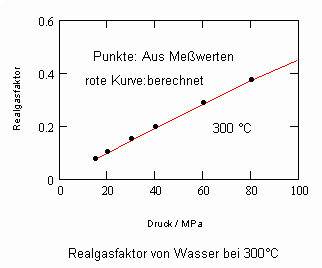
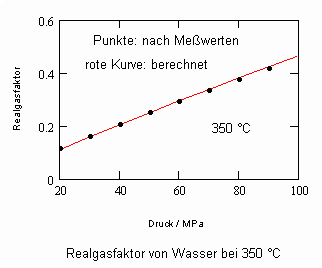
Die nachfolgenden Diagramme für Realgasfaktoren solch wichtiger Stoffe wie Wasser und Kohlenstoffdioxid bei verschiedenen Temperaturen können die gute Übereinstimmung zwischen Rechnung mit obiger Gleichung und Meßwerten zeigen.
Wasser- flüssig:
Kohlenstoffdioxid CO2- flüssig:
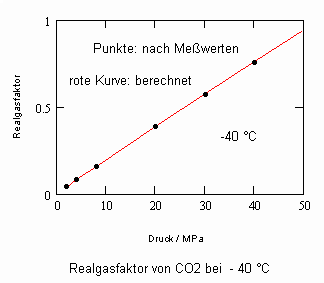
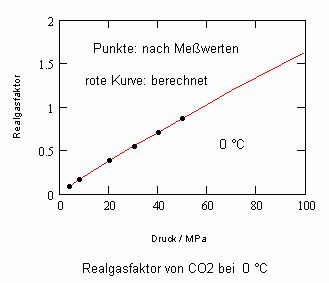
Die gute Übereinstimmung zwischen Rechnung und den Werten aus Versuchsdaten ist für die wichtigen Beispiele Wasser und Kohlenstoffdioxid ersichtlich. Ein weitgehend linearer Verlauf des Realgasfaktors Z in Abhängigkeit vom Druck auf einer Isotherme ist ersichtlich.
Für viele Stoffe, auch technisch wichtige Stoffe, ist die Druckabhängigkeit von Flüssigkeitsdaten noch gar nicht bekannt. Nur für absolut wichtige Stoffe- wie z. B. Wasser, Kohlenstoffdioxid, Methan, Ethylen, Propan, Butan, Stickstoff, Ammoniak, Sauerstoff- sind Realgasfaktoren druckabhängig bei verschiedenen Temperaturen als allgemein zugängige Daten (ohne evtl. vorhandene Angaben aus gebührenpflichtigen Datenbanken) auf der Grundlage von Meßwerten erfaßt. Mit der o. gen. Flüssigkeitszustandsgleichung besteht nun die Möglichkeit, den Verlauf des Realgasfaktors einer Flüssigkeit zumindest als Näherung zu erfassen, wenn allein nur die pvT- Daten des normalen Siedepunkts des Stoffes vorliegen (oder auch nur das molare Volumen bei einer Temperatur niedrigen Dampfdrucks).
Die eingangs gen. Flüssigkeitszustandsgleichung wird gelöst, indem bei vorgegebenem Druck und vorgegebener Temperatur das jeweilige molare Volumen gesucht wird. Bei der überwiegenden Zahl der Lösungen liegt jeweils nur ein Volumenwert vor, so daß als Realgasfaktor immer nur ein Wert Z = pv/RT entsteht. Interessanterweise existieren aber auch p,T- Zustände von Flüssigkeiten, für die sich nach obiger Gleichung nicht nur eine Lösung für das molare Volumen ergibt, sondern sogar zwei! Das bedeutet, daß es in solchen Flüssigkeitszuständen zumindest mathematisch auch zwei Realgasfaktor- Werte gibt.
An den Beispielen Wasser und Kohlenstoffdioxid soll das näher erläutert werden.
Für Wasser bei 300 °C und einem Druck von 10 MPa ergibt sich rechnerisch ein Realgasfaktor Z1 = 0.049, der mit dem entsprechenden Wert 0.051 auf der Grundlage von Meßwerten gut übereinstimmt. Außerdem ergibt sich aber auch noch ein zweiter Wert Z2 = 0.186. Bei einem Druck von 15 MPa ebenfalls bei 300 °C ist Z1 = 0.073 und Z2 = 0.32 feststellbar. Der Wert Z1 stimmt gut mit dem auf der Basis von Meßwerten sich ergebenden Realgasfaktor 0.078 überein. Nur im Bereich der Temperatur von 300 °C und Drücken von ca. 10 bis 15 MPa ist eine zweite Lösung Z2 überhaupt feststellbar. Alle anderen untersuchten Wasser- Zustände von 100 bis 350 °C und Drücken bis 100 MPa haben immer nur eine Z- Lösung, die mit den Werten nach Messungen gut übereinstimmen.
Die Frage ist: Was bedeutet die Lösung Z2, die nur in einem eng begrenzten Druck- und Temperaturbereich erklärt ist?
Auch für Kohlenstoffdioxid sind ähnlich wie bei Wasser in einem eng begrenzten p,T- Bereich zwei Lösungen der angewendeten Flüssigkeitszustandsgleichung feststellbar, so daß für bestimmte p,T- Zustände jeweils zwei Realgasfaktoren genannt werden müssen. Für Kohlenstoffdioxid z. B. bei -40 °C und einem Druck von 2 MPa ist Z1 = 0.04 und Z2 = 0.4 feststellbar. Der Wert Z1 stimmt mit dem mit Meßwerten ermittelten Wert o.o405 gut überein. Bei einer Temperatur von 0 °C und einem Druck von 4 MPa ergibt sich Z1 = 0.0845. Dies stimmt gut dem Wert 0.08305 überein,der sich nach Meßwerten ergibt. Für einen zweiten Wert gilt Z2 = 0.172. Ähnlich wie im Fall Wasser ist die zweite Lösung in einem nur engen Zustandsbereich erklärt (ca. von -40°C bis 0 °C und relativ niedrigen Drücken).
Auch hier ist die Frage zu stellen, was bedeutet die zweite Lösung Z2, die nur in einem engem Druck- und Temperaturbereich erklärt ist?
Es gibt nur zwei Erklärungsmöglichkeiten. Prinzipiell besteht die Möglichkeit, daß die Lösung Z2 ohne eine physikalische Bedeutung allein nur durch die mathematische Strucktur der o.gen. Flüssigkeitszustandsgleichung zu Stande kommt. Sicherlich muß man diesen Fall präferieren. Die andere Möglichkeit würde folgendes bedeuten: Für einen bestimmten vorgegebenen Druck und eine bestimmte vorgegebene Temperatur einer Flüssigkeit können zwei molare Volumenwerte existieren, so daß in diesem Fall zwei Realgasfaktoren feststellbar sind. Dies würde allerdings weiter bedeuten, daß in einem engen p,T- Zustandsbereich einer Flüssigkeit zwei Modifikationen des Stoffes mit zwei unterschiedlichen Dichten existieren können – ρ1 = M/v1, ρ2 = M/v2 (M- relative Molmasse g/mol). Sollte solch eine Möglichkeit tatsächlich bestehen? Es ist sehr fraglich. Andererseits ist die evtl. Existenz der beiden Flüssigkeitsmodifikationen in einem jeweils nur sehr engen p,T- Bereich erklärt, zu dem in Bezug auf eine zweite Modifikation wegen ihrer Unwahrscheinlichkeit bisher gar keine Untersuchungen vorliegen können.
Was sollte getan werden?
Experimente z.B. mit Wasser bei ca. 300 °C und Drücken um 10 bis 15 MPa könnten darüber aufklären, ob es eine zweite Flüssigkeitsmodifikation entsprechend der obigen Flüssigkeits- Zustandsgleichung überhaupt gibt. Der Autor dieses Artikels ist dazu nicht in der Lage. Gibt es fachlich Interessierte, die die Gültigkeit und Aussagekraft der gen. Flüssigkeits- Zustandsgleichung mit den dazu notwendigen Technik- Einrichtungen überprüfen könnten und wollen? Allerdings besteht das Risiko, nur bestätigt zu bekommen, daß es nur die eine Flüssigkeitsmodifikation gibt. Falls allerdings bestätigt werden sollte, daß es in einem engen p,T- Bereich eine zweite Flüssigkeitsmodifikation geben kann, ist der wissenschaftliche Gewinn erheblich.