Für reale Gase wurde mit Gesetzmäßigkeiten kritischer Phänomene die Funktion
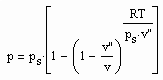 (1)
(1)
formuliert. Dabei ist p der Druck/MPa, ps der Dampfdruck/MPa, T die absolute Temperatur/K, v das Volumen/cm³/mol, v“ das Sättigungsdampfvolumen cm³/mol und R die allgemeine Gaskonstante 8.314 J/mol K. Die Funktion (1) ergibt sich allein nur mit Kenntnissen über kritische Phänomene ohne Voraussetzung und Anwendung von physikalischen Theorien, die die Anwendung der van der Waals-Thermodynamik und ihren empirischen Weiterentwicklungen, der physikalisch begründeten Virialgleichung und ihren Weiterentwicklungen oder gar der sogen. molekularen Thermodynamik und damit auch deren Vorstellungen über den Molekülaufbau des jeweiligen Stoffes und der molekularen Wechselwirkungen voraussetzen. Die Grundlage dieser Funktion ist nicht die bisherige Thermodynamik, sondern allein nur ein thermodynamisches Modell begründet mit kritischen Phänomenen.
Für Gase besteht neben der physikalisch begründeten van der Waals- Gleichung die ebenfalls physikalisch begründete Virial-Gleichung . Grundlage der Virialgleichung ist die Taylor- Entwicklung des Realgasfaktors Z=pv/RT in eine Reihe für die Dichte 1/v→0. Als Reihenentwicklung wird
Z=1+B/v+C/v²+…… (2)
erhalten. Die Koeffizienten B,C,….werden als 2., 3. usw. Virialkoeffizient bezeichnet. Sie sind nur temperaturabhängig.
Die Berechnung von Zustandsdaten realer Gase gelingt mit der Virialgleichung als Näherung, wenn zumindest der 2. und evtl. 3. Virialkoeffizient bekannt ist. Man sagt, die Funktion Z= 1+B/v ist als Näherung ausreichend bis zu Gasdichten von ca. 0.5 ρk, die Funktion Z= 1+B/v+C/v² bis zu Dichten von ca. o.75 ρk (ρk- kritische Dichte).
Die der o.gen. Funktion (1) entsprechenden Virialkoeffizienten können berechnet werden. Die Kenntnis des 2. Virialkoeffizienten z. B. ist aus folgenden Gründen sinnvoll: Der 2. Virialkoeffizient eines Stoffes nämlich steht mit dem Wechselwirkungspotential der zwischenmolekularen Kräfte zweier Moleküle eines Stoffes in Verbindung. Wenn man den 2. Virialkoeffizienten kennt, muß es der Theoretischen Physik möglich sein, Aussagen zu der wichtigen Potentialfunktion der zwischenmolekularen Kräfte eines Stoffes abzuleiten. Die Statistische Thermodynamik formuliert für den 2. Virialkoeffizienten
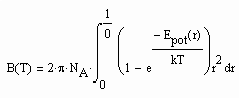 . (3)
. (3)
Dabei ist NA die Avogadrosche Konstante, Epot ist das Potential der zwischenmolekularen Kräfte, k ist die Boltzmann- Konstante und r ist der radiale Abstand zweier Moleküle des jeweiligen Stoffes. Wenn also der Virialkoeffizient B(T) bekannt ist, können Aussagen zu dem molekulartheoretischen sehr grundlegenden Potentialverlauf Epot(r) getroffen werden. Und wenn das möglich ist, ist letzlich auch eine Aussage zum Potentialverlauf zwischenmolekularer Kräfte verschiedener Stoffe möglich, so daß damit dann Gemischeigenschaften erfaßt werden können. Die hierzu erforderlichen weiteren Untersuchungen können hier allerdings nicht dargelegt werden.
Der zur näheren Bestimmung des Potentials zwischenmolekularer Kräfte erforderliche 2. Virialkoeffizient, der sich entsprechend (1) und (2) ergibt, lautet
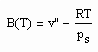 . (4)
. (4)
Am Beispiel Wasser soll gezeigt werden, daß der nach (4) berechnete 2. Virialkoeffizient durchaus dem nach Meßwerten entspricht.

Mit Hilfe der o.gen. Taylor- Entwicklung ist ersichtlich, daß für über alle Grenzen wachsendes Volumen
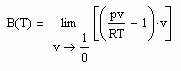 (5)
(5)
gilt (s. z.B. J. Gmehling, B. Kolbe: Thermodynamik, VCH, 1992). Damit besteht auf einer Isothermen die Beziehung
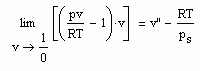
(6).
Das ist aus folgendem Grund interessant: Der Grenzwert auf der linken Gleichungsseite wird experimentell bestimmt, indem bei T=konstant bei vorgegebenem Druck für p gegen O das jeweils zugehörige Volumen gemessen wird. Dies sind dann alles Stoffdaten ohne Bezug zu den Sättigungsdaten v“ und ps. Und trotzdem besteht laut der obigen Gleichung ein Zusammenhang mit dem Sättigungsvolumen v“ und dem Dampfdruck ps! Eine Information zu v“ und ps ist also in dem o.gen. bei verschwindenden Druck experimentell bestimmbaren Grenzwert bereits enthalten.
So wie es möglich war, für reale Gase die Zustandsfunktion (1) entsprechend Gesetzmäßigkeiten kritischer Phänomene abzuleiten, zeigt es sich, daß auch für Flüssigkeiten eine druckexplizite allgemeine Zustandsfunktion ebenfalls nur auf der Grundlage kritischer Phänomene in der Form p = p(v,T) als Näherung bestimmt werden kann. Kenntnisse zum Molekülaufbau und zu Wechselwirkungen innerhalb der Moleküle und zwischen den Molekülen des Materials sind dabei erstaunlicherweise gar nicht erforderlich. Allerdings sind die kritischen Daten pk, vk, Tk und das Flüssigkeitssättigungsvolumen v‘ als bekannte Parameter vorauszusetzen. Die Ableitung der gen. Zustandsfunktionen für reale Gase und für Flüssigkeiten durch Auswertung von Gesetzmäßigkeiten kritischer Phänomene soll mit einer entsprechenden Veröffentlichung 2013 gezeigt werden.