Die für Stoffeigenschaften maßgeblichen Wechselwirkungen zwischen den Molekülen und Atomen eines Stoffes haben eine Reichweite von nur einigen Molekül- bzw. Atomdurchmessern. Im kritischen Zustand und in seiner Nähe entsteht allerdings ein universelles Verhalten physikalischer Größen wegen des Eintretens sogen. „kritischer Fluktuationen“, die sich wie eine beträchtliche Vergrößerung der sogen. Korrelationslänge auswirken. Es entstehen kritische Phänomene. Dies hat zur Folge, daß Eigenschaften völlig unterschiedlicher Stoffe sich im nahkritischen Zustand nach analog gleichen Gesetzmäßigkeiten verhalten, so als ob individuelle Stoffeigenschaften verschwinden.
Kritische Phänomene sind z. B. erklärt für
– den Dichtesprung zwischen flüssiger und dampfförmiger Phase
– die Differenz vom Druck zum kritischen Druck bzw. von der Dichte zur kritischen Dichte auf der kritischen Isotherme
– Kompressibilitäten
-Wärmekapazitäten
– magnetische Zustände (Suszepilitäten) bei verschwindendem Feld.
Die Aussagen der klassischen Theorien treffen für nahkritische Zustände realer Gase und Flüssigkeiten nicht zu.
Die heutigen thermischen Zustandsgleichungen als Grundlage der Berechnung von Stoffdaten für Flüssigkeiten und Gasen beruhen alle letzlich auf der physikalisch begründeten van der Waals- Gleichung , der Virialgleichung, auf Ansätzen der Statistischen Thermodynamik und vor allem immer wieder auf Parameter – Anpassungen empirischer Berechnungsgleichungen an Meßwerte. Der Aufwand ist hoch. Die empirische Vielfalt ist kaum noch überschaubar. Sie ist mit hohem Aufwand zur Bestimmung der Meßwerte verbunden. Die unter Physikern manchmal ironisch geäußerte Kritik, daß die sogen. „halbempirischen Zustandsgleichungen“ und andere rein empirische Gleichungen (z. B. die für nahkritische Zustände ) ja höchstens ein empirisch erforderliches Niveau von wenigstens nur zur Hälfte oder weniger erfüllen, charakterisiert die Situation.
Die Theoretische Physik muß trotz der unzweifelbaren verfahrenstechnischen Empirie- Erfolge der letzten Jahrzehnte Richtschnur im Labyrinth der Möglichkeiten bleiben. Die Suche nach physikalisch begründeten neuen Ansätzen mit geringen empirischen Anteilen sollte gerade auf dem Gebiet der Berechnung von Druck p, Volumen v, Temperatur T- Daten aktuell sein und bleiben.
Die Theoretische Physik formuliert eine sogenannte Universilatitätshypothese: „Die kritischen Exponenten sind fast universell, d. h. für alle thermodynamischen Systeme gleich.“ (s. Nolting: Grundkurs Theoretische Physik, Statistische Physik, Springer Verlag 2004), (R.B. Griffiths: Phys. Rev.Lett.24, 1949 (1970)). Diese Hypothese wird unterdessen als bewiesen betrachtet (Renormierungsgruppentheorie von K. Wilson).
Entsprechend der Universalitätshypothese haben also z. B. die kritischen Exponenten β und δ der kritischen Phänomene – Dichtesprung und Druck- bzw. Dichtedifferenz auf der kritischen Isotherme für völlig verschiedene Stoffe die jeweils fast gleichen Werte. Diese sehr erstaunliche Eigenschaft wird als Folge einer beträchtlichen Vergrößerung der Korrelationslänge von Teilchenwechselwirkungen in der Nähe des kritischen Punktes erklärt.
Im Ergebnis der für den Dichtesprung und die kritische Isotherme durchgeführten Untersuchungen erweist es sich als möglich, wesentliche Schlußfolgerungen zum Verhalten realer Gase und Flüssigkeiten in der Umgebung des kritischen Punktes und auch für Zustände weit unter der kritischen Temperatur abzuleiten.
Und hier ist das theoretische Problem.
Die Gesetzmäßigkeiten kritischer Phänomene sind nur erklärt in einem engem Intervall von Zustandsdaten um den kritischen Punkt. Die Erweiterung des Gültigkeitsbereichs von Gesetzmäßigkeiten kritischer Phänomene weiter entfernt vom kritischen Punkt, also nicht nur für Zustände in unmittelbarer Nähe des kritischen Punktes, dürfte deshalb unmöglich sein. Aber das ist nicht der Fall. Denn es zeigt sich bei der Auswertung von Meßdaten an den verschiedensten Stoffen, daß es möglich ist, Gesetzmäßigkeiten kritischer Phänomene zur Bestimmung von Zustandsdaten auch weit entfernt von der kritischen Temperatur und vom kritischen Druck anzuwenden. Die Ergebnisse stimmen dann durchaus mit Meßwerten überein.
In Auswertung solcher Ergebnisse der Untersuchung von Stoffwerten wurde als Hypothese die Erweiterbarkeit der Gesetzmäßigkeiten kritischer Phänomene auf Zustände weiter entfernt vom kritischen Punkt vorausgesetzt. Durch die vorliegenden Ergebnisse mit Untersuchungen an konkreten Stoffdaten ist diese Hypothese als berechtigt dargestellt.
Die physikalische Begründung allerdings fehlt.
Das Anliegen dieser Schrift ist es, theoretische Physiker und Theoretiker der physikalischen Chemie und auch theoretische Kenntnisse besitzende Verfahrenstechniker zu veranlassen, die Gründe der Erweiterbarkeit von Gesetzmäßigkeiten kritischer Phänomene weit über nahkritische Verhältnisse hinaus zu suchen und zu benennen.
Ergebnisse bisheriger Untersuchungen auf der Grundlage der o.gen. Hypothese sind die folgenden.
Für reale Gase niedriger bis hoher Drücke ergibt sich auf der gen. Grundlage ein funktionaler Zusammenhang zwischen dem Druck p und dem molaren Volumen v auf einer Isotherme der Temperatur T entsprechend der Gleichung
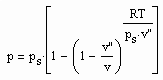 , (I)
, (I)
wobei ps der Dampfdruck, v“ das molare Sättigungsdampfvolumen und R die allgemeine Gaskonstante ist.
Es zeigt sich weiter, das es mit den auf der Grundlage der Theorie kritischer Phänomene gewonnenen Ergebnisse möglich ist, eine allgemeine Beziehung abzuleiten, die die Berechnung des molaren Volumens v“ trocken gesättigten Dampfes bei bekanntem Dampfdruck ps als grobe Näherung gestattet:
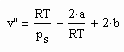 . (II)
. (II)
Dabei sind a und b die Parameter der klassischen van der Waals- Gleichung realer Gase, die nur von den kritischen Daten Tk (kritische Temperatur) und pk (kritischer Druck) abhängen. Die sinnvolle Anwendung dieser Gleichung ist für Zustände näherungsweise von niedrigen bis hohen Temperaturen gegeben, nicht aber für nahkritische Verhältnisse.
In Auswertung der zu kritischen Phänomenen durchgeführten Untersuchungen ergab sich weiterhin die Gleichung![]() , (III)
, (III)
die von niedrigen bis zu hohen Temperaturen gilt. Dabei ist der kritische Exponent β mit dem Wert 1/3 vorausgesetzt. Kv ist die sogen. Dichtesprungkonstante, die einfach berechnet werden kann. Die obige Gleichung (III), die dem Dichtesprung zwischen siedender Flüssigkeit des Volumens v‘ und dem Sattdampfvolumen v“ entspricht, ermöglicht die Berechnung des Sättigungsvolumens v‘ der Flüssigkeit bei gegebener Temperatur, wenn v“ bereits mit (II) berechnet werden konnte. Für das Siedevolumen der Flüssigkeit ergibt sich näherungsweise
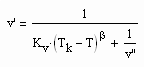 . (IV)
. (IV)
Damit sind bei vorgegebener Temperatur und bekanntem Dampfdruck die Sättigungsvolumina v‘ und v“ eines Stoffes näherungsweise berechenbar, wenn die kritischen Daten bekannt sind.
Für Zustände kurz unter der kritischen Temperatur bestehen wegen der am kritischen Punkt sich beträchtlich vergrößernden Fluktuationen veränderte Bedingungen, die zu anderen sich aus (III) ableitbaren Berechnungsgleichungen führen. Damit sind dann sogar die Sättigungsvolumina v‘ und v“ und auch der Dampfdruck ps für Temperaturen kurz unter der kritischen Temperatur als Näherungen berechenbar.
Speziell für Flüssigkeiten in nahkritischen und auch bis weit unterkritischen Zuständen kann eine Zustandsfunktion abgeleitet werden, die die Berechnung des jeweiligen Flüssigkeitsvolumens bei vorgegebenem Druck und vorgegebener Temperatur als Näherung gestattet. Damit ist dann das Flüssigkeitsverhalten eines Stoffes für das gesamte Existenzgebiet vom Dampfdruck sogar bis zu höheren Drücken im 10 MPa- Bereich und teilweise darüber erfaßt- wie Nachrechnungen an gut vermessenen Stoffbeispielen zeigen.
Alle bisherigen Ansätze zu einer allgemeinen Theorie der Flüssigkeiten gehen letztlich vom jeweiligen Molekülaufbau, von den zwischenmolekularen Wechselwirkungen, von molekulartheoretischen Ansätzen der Quantenmechanik und Statistischen Thermodynamik bis hin zur Statistik mit Monte-Carlo- Modellen usw. aus. Die gesuchte Aussage zu einer möglichst allgemeingültigen Erklärung und mathematischen Fassung der pvT- Eigenschaften von Flüssigkeiten wurde so bisher nicht gefunden.
Für die bei der Auswertung kritischer Phänomene gefundene allgemeine Zustandsfunktion von Flüssigkeiten ist als Ausgangspunkt zur Beschreibung und Erklärung des Verhaltens von Flüssigkeiten nur der kritische Punkt eines Stoffes mit seinen kritischen Phänomenen erklärt, indem die sonst nur in einem engen Bereich um die kritische Temperatur gültigen Gesetze kritischer Phänomene auf Temperaturen weit unterhalb der kritischen Temperatur übertragen werden. Die physikalische Erklärung dazu fehlt!